Na czym polega różnica między postrzeganiem kwantowym a klasycznym pól grawitacyjnych, prędkości i przyśpieszenia? Przedstawię tę różnicę na prostym przykładzie - okręgu. Oto teza, którą postaram się udowodnić:
TEZA I
1. Wszystkie okręgi możemy uznać za różne okręgi, pod warunkiem, że przypisujemy im krzywiznę „zerową" euklidesowej płaszczyzny odniesienia gdy
L = 2 Pi 1
czyli promień przyrównujemy na przykład do jedności lub danej stałej - określając w ten sposób poziom klasyczny obserwacji.
2. Wszystkie okręgi oraz punkt możemy uznać za różne stany jednego i tego samego okręgu o zmiennej krzywiźnie, gdy
L = k * 2 Pi r
w ten sposób określamy kwantowy sposób obserwacji.
W „wymiarze krzywizny" możliwa jest taka transformacja okręgu, że może on zostać sprowadzony do stanu, który określimy jako punkt materialny. Rys. 1
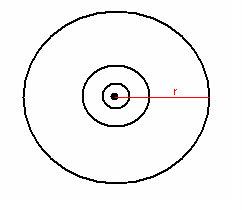
Nowe podejście do rozumienia pojęcia krzywizny oraz wprowadzenie nowego wymiaru krzywizny.
Dotychczasowo obowiązujący pogląd mówi nam, że zmiana krzywizny przestrzeni zachodzi w ten sposób, że na przykład okrąg o geometrii
L = 2 π r
znajdujący się na płaszczyźnie o krzywiźnie zerowej, przeniesiony na powierzchnię kuli zmienia swoją krzywiznę na dodatnią, a to dlatego, że owa płaszczyzna charakteryzuje się krzywizną dodatnią. Zmiana zachodzi poprzez wytyczenie nowej, nieeuklidesowej płaszczyzny odniesienia w ten sposób, że obwód okręgu „L" oraz promień „r" pozostają bez zmian, ale są umiejscowione na powierzchni kuli o krzywiźnie dodatniej lub tak zwanej powierzchni „siodła" o krzywiźnie ujemnej. Rys. 2
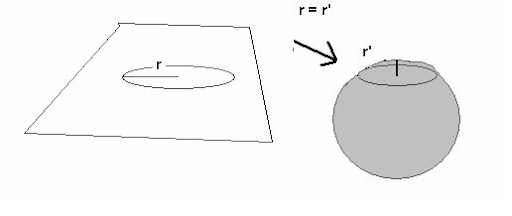
Czy do określenia zmiennej krzywizny obiektu konieczna jest płaszczyzna odniesienia o zróżnicowanych krzywiznach? Wystarczy wyobrazić sobie choćby gumkę aptekarską (nie tyle ze względu na jej sprężystość, ile na fakt utrzymywania „okrągłości" przy odkształcaniu), którą jako okrąg możemy odkształcać i skręcić na przykład do postaci dwóch okręgów, a potem obserwować przestrzenne zmiany jego kształtu na płaszczyźnie euklidesowej.
Czy możliwe byłoby zaobserwowanie zmiennej krzywizny takiego obiektu przy użyciu euklidesowej płaszczyzny odniesienia? Odpowiedzieć jest pozytywna.Dlatego proponuję do problemu podejść inaczej i potraktować okrąg nie jako figurę, lecz właśnie obiekt i poszukać sposobu obserwacji zmian krzywizny samego obiektu na płaszczyźnie euklidesowej. Pozwoliłoby to - przy zastosowaniu nowej metody obserwacji - na stopienie przedmiotu (okręgu jako obiektu obserwacji) i podmiotu (obserwatora) w jedno, sprowadzając wielowymiarowy obiekt - zjawisko (skręcania gumki czyli zmiany geometrii okręgu) do dwuwymiarowej płaszczyzny obserwatora (wielowymiarowy przedmiot kwantujemy do poziomu płaszczyzny obserwacji dwuwymiarowego podmiotu) poprzez zastosowanie parametrów dodatkowego wymiaru - wymiaru krzywizny.
Topologia jest pojęciem matematycznym obejmującym takie właściwości przestrzeni, które nie ulegają zmianie w wyniku skręcania, rozkręcania, zginania, zakrzywiania... Dlatego potrzebna jest prosta metoda, która tego typu działania (podstawowe w grawitacji kwantowej) mogłaby opisywać.
Nowa metoda wymaga przyjęcia zasady zmienności stanów okręgu, co by znaczyło, iż istnieje jakiś jeden powiedzmy meta-okrąg, który może zostać przestrzennie tak odkształcony, że zmienia on swoją krzywiznę na dodatnią lub ujemną czyli może znajdować się w różnych stanach w wyższych wymiarach, poza euklidesową płaszczyzną odniesienia. Będzie to inny sposób przeniesienia niż transformacje Lorentza.
Na płaszczyźnie euklidesowej obserwowalibyśmy wtedy różne okręgi (o zmiennym promieniu i obwodzie) jako różne stany jednego meta-okręgu, a każdy okrąg na płaszczyźnie euklidesowej byłby jedynie czymś w rodzaju rzutu lub cienia - stanu wielowymiarowego meta-okręgu. Zasadę zmienności stanów okręgu określa następująca teza.
TEZA II
1. Każdy okrąg może znajdować się w stanie o krzywiźnie dodatniej lub ujemnej, gdy zostaje skwantowany czyli przeniesiony do wymiaru krzywizny.
2. Każdy okrąg o różnym promieniu i różnym obwodzie może być jednym i tym samym stanem meta-okręgu znajdującego się w wyższej wymiarowości, innej niż wymiarowość euklidesowej płaszczyzny odniesienia.
Aby udowodnić tę tezę należy znaleźć możliwość przedstawiania na płaszczyźnie euklidesowej różnych stanów meta-okręgu jako różnych okręgów o zmiennej krzywiźnie. Poniżej przedstawiam taki sposób. Na pierwszym rysunku mamy okrąg L = 2 π r, gdzie r = 1 czyli
L = 2 π 1
Ten okrąg znajduje się w stanie A.
Rys. 3
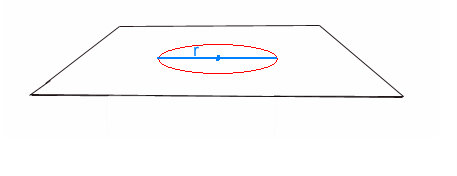
Następnie okrąg przechodzi do innego stanu, powiedzmy B, który może być obserwowany na powierzchni kuli!
Rys. 4
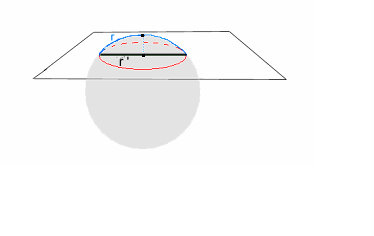
Tego typu przetworzenie wyjaśnia się na przykład w OTW w następujący sposób: " koło na powierzchni kuli ma mniejszy obwód niż koło wykreślone na kartce papieru (powierzchni euklidesowej). A większy będzie miało narysowany na powierzchni siodła". (...) Takie skrócenie obwodu to nic innego jak skrócenie Lorentza. Brian Greene „Piękno wszechświata". W OTW, kiedy mamy do czynienia z ruchem przyśpieszonym - przykład z Chudym i Rudym na karuzeli (tamże str.70), B.G. tłumaczy, że im większa odległość Rudego od środka koła mierzącego długość promienia, tym Chudy będzie obserwował na obwodzie (mierzył linijką ) coraz większe przyśpieszenie. Obwód przyjęto za zmienny, a promień za stały.
Dlaczego obwód nie ulega takiemu samemu skróceniu jak linijka Chudego, a więc dlaczego Chudy nie otrzymuje takiego samego wyniku, jak zakłada Rudy? Skrócenie Lorentza obwodu karuzeli miałoby znaczenie tylko wtedy, gdybyśmy porównywali właściwości karuzeli znajdującej się w ruchu i w spoczynku. Oto odpowiedź. Czyli możemy dokonywać różnych obserwacji: zmniejszenia lub zwiększenia obwodu bez skracania promienia albo skrócenia lub wydłużenia promienia z zachowaniem stałego obwodu. Będzie to zależało od przyjętego sposobu obserwacji.
A teraz stan B z rys. 4 sprowadzamy z powrotem na płaszczyznę euklidesową. Rys. 5
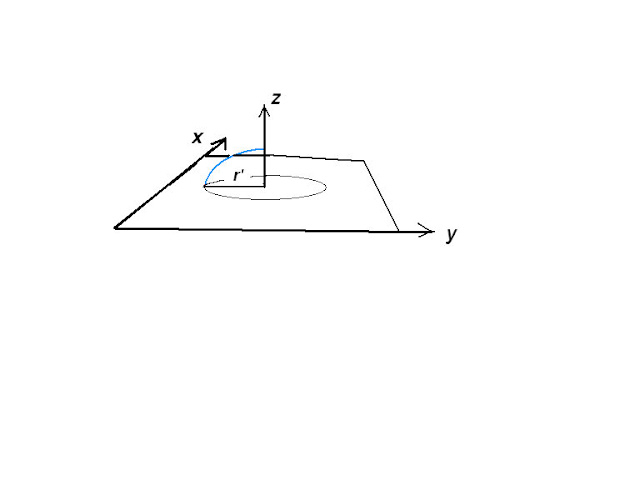
Dlaczego tak się dzieje, że teraz obwód wydaje nam się mniejszy i promień także? I co naprawdę dzieję się z obwodem? Uległ odkształceniu, podobnie jak promień, ale co to za odkształcenie? Okrąg zmienił swoją krzywiznę na dodatnią, a promień na ujemną. Przyśpieszenie, które się pojawia na obwodzie jest spowodowane skróceniem promienia w obserwacji prowadzonej na płaszczyźnie euklidesowej!
Zmniejszenie obwodu i promienia względem płaszczyzny euklidesowej następuje jednocześnie w wymiarze krzywizny. Zmiana obwodu - skrócenie Lorenca w powyższym przykładzie - jest wynikiem przeniesienia obserwacji ponad dwuwymiarowego stanu koła do poziomu dwuwymiarowej euklidesowej płaszczyzny o krzywiźnie zerowej. Skrócenie Lorentza jest zatem próbą opisania takiego stanu koła, który ma miejsce w trójwymiarowej przestrzeni i przedstawienia go na dwuwymiarowej płaszczyźnie. Jest próbą sprowadzenia obiektu zakrzywionego na płaszczyznę euklidesową. Jest to możliwe dzięki zastosowaniu prostego wzoru:
k * 2 Pi r = 2 Pi 1
W przypadku zmiany wartości obwodu na mniejszą (L < 2 Pi 1) i braku zmiany promienia (r = 1) mamy do czynienia z przestrzenią o krzywiźnie dodatniej.W przypadku zmiany wartości obwodu na większą (L > 2 Pi 1) i braku zmiany promienia (r = 1) mamy do czynienia z przestrzenią o krzywiźnie ujemnej.Ale także w przypadku zmiany długości promienia na mniejszą (r < 1) i braku zmiany obwodu (L = 2 Pi 1) mamy do czynienia z przestrzenią o krzywiźnie dodatniej, a w przypadku zmiany długości promienia na większą (r > 1) i braku zmiany obwodu (L = 2 Pi 1) mamy do czynienia z przestrzenią o krzywiźnie ujemnej.
A w podanym przeze mnie przykładzie (rys 5) mamy JEDNOCZESNĄzmianę:
Obwód zostaje zmniejszony (krzywizna dodatnia), a promień zostaje skrócony (krzywizna ujemna zróżnicowana wzdłuż promienia).
Przyjrzyjmy się zatem dokładnie takiemu przekształceniu okręgu, który nie zmienia swojego obwodu.
Geometria okręgu obserwowana w wymiarze krzywizny dodatniej a jego fizyczne właściwości.
Weźmy gumkę aptekarską. Ma ona obwód L = 2 pi r i znajduje się w stanie o „krzywiźnie zerowej". Przyjmijmy, że promień jest równy jedności r = 1. Skręćmy teraz gumkę tak, żeby jej obwód utworzył dwa okręgi czyli jeden podwójny. A teraz skręćmy tak, by utworzył potrójny... itd. Teoretycznie taką gumkę można by skręcać aż do punktu - malutkiej kulki. Można powiedzieć, że dostarczamy jej energii, a ona zmienia swoją geometrię - skraca się promień ulegający skrętom i zwiększa się geometryczna krzywizna gumki. Jeśli przestaniemy dostarczać jej energii, to gumka zacznie rozwijać się sama do postaci o „najniższej energii" i „krzywiźnie zerowej". Do swojego „stanu podstawowego" - można by powiedzieć. Skręcając gumkę zauważymy, że w stanie „podstawowym" nieskręcona gumka leżąca na stole jest styczna z blatem stołu czyli z naszą euklidesową płaszczyzną odniesienia, ale im bardziej jest skręcona tym większe wartości zajmuje w dodatkowym, trzecim prostym wymiarze przestrzennym. Jednak w trakcie eksperymentu gumka zmienia swoją geometrię w „wymiarze krzywizny". Wartość krzywizny gumki leżącej na blacie stołu jest „zerowa". Następnie obserwujemy, że przechodzenie od pierwszego stanu gumki o geometrii
2 π 1
do stanu o geometrii
4 π ½
(podwójnego skrętu) odbywa się w przestrzeni poza płaszczyzną euklidesową. Czyli możnaby je przedstawić na hiperpłaszczyznie. Rys. 6
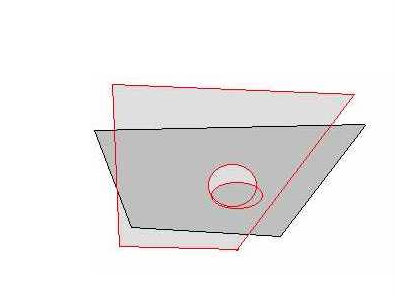
Zmiana ta powoduje zmianę nie tyle przestrzeni zajmowanej przez gumkę, co zmiane krzywizny samej gumki. W jaki sposób możemy obserwować te zmiany stanów okręgu na płaszczyźnie euklidesowej?
Stany fazowe okręgu
Na dwuwymiarowej płaszczyźnie euklidesowej możemy obserwować teraz jedynie jeden okrąg, który jest „połówką" skręconego okręgu. Rys. 7
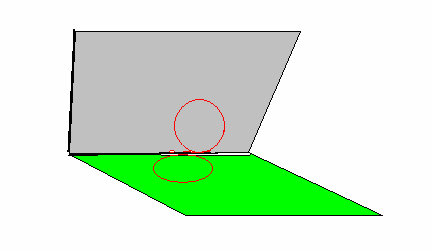
Obserwator może dokonywać obserwacji tylko na jednej z tych płaszczyzn (zielona lub szara). Zmiana krzywizny zachodzi w następujący sposób:
z
2 π 1
na
2 x 2 π ½
Wymusiło to "zapętlenie" (skręt) pojedyńczego okręgu do podwójnego okręgu o promieniu o połowę mniejszym. Dwa małe okręgi są równoważne z jednym dużym, ale duży i dwa małe różnicuje inna wartość krzywizny przestrzennej. Okrąg uległ „skokowi kwantowemu" w wymiarze krzywizny z 2 π 1 do 4 π ½ , więc połowa gumki pozostaje na dwuwymiarowej płaszczyźnie, a druga połowa znajduje się w „zaświecie wymiarowym".
Dalej mamy różne stany meta-okręgu o wzorze:
L = k * π 2 r
Nadal promień jest równy jedności r = 1. Jak zakrzywia się okrąg? Kiedy obserwujemy skrócenie promienia okręgu jako danego stanu okręgu, przyjmujemy, że spowodowane jest ono kolejnymi „zawinięciami" tego okręgu w dodatkowym wymiarze krzywizny.
Przy okazji tego zjawiska występuje geometryczne zwiększenie krzywizny polegające na zwielokrotnianiu się okręgów:
2 x 2 π 1/2,
3 x 2 π 1/3,
4 x 2 π 1/4
itd...
czyli
2 π 1 = k * 2 π r
w wymiarze krzywizny.W ten sposób wartości wymiaru krzywizny określają zmienne wielokrotności k liczby wobec liczby π.
Przyjrzyjmy się stanowi, który możemy zapisać jako
3 x 2 π r/3
Teraz mamy trzy płaszczyzny: 2 π r +2 π r + 2 π r = L. Rys. 8
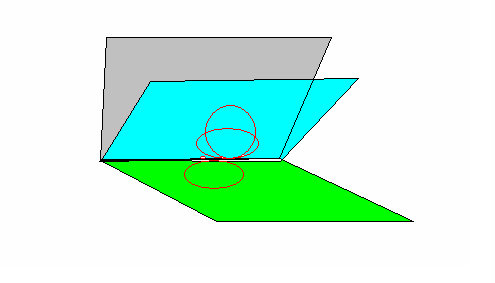
Ten stan możemy zapisać jako: L = 3 x 2 π 1/3. Jest to stan fazowy (liniowy), podobnie jak inne stany tego typu:
2 π 1,
2 x 2 π ½ ,
4 x 2 π ¼,
5 x 2 π 1/5 ,
6 x 2 π 1/6 ,
7 x 2 π 1/7 itd.
Każdy stan „fazowy" staje się ubezwzględniony na płaszczyźnie euklidesowej.Przyjrzyjcie się przekształceniom okręgu:
L = 2 π r +2 π r = 4 π 2 r = 8π r
Teraz pod obwód L podstawmy wartość okręgu jako ubezwzględnionego czyli r przyrównamy do jedności r = 1, stąd:
2 π 1 = 8 π r
I obliczamy promień:
r = 2 π 1/ 8 π
r = ¼
Kiedy uwzględniamy zmiany krzywizny geometrii okręgu, zobaczymy, że jego promień został skrócony. Rys. 9
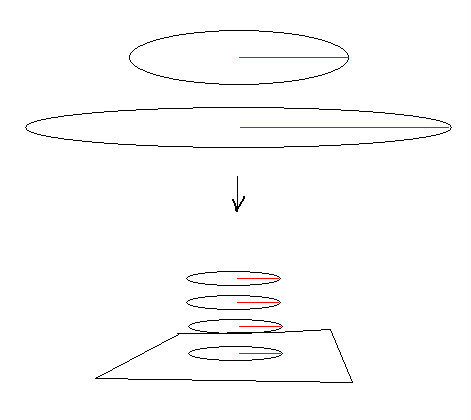
Zmiana wielokrotności liczby pi wraz ze zmianą długości promienia zachodzi w sposób ciągły, ale nie jest to w tym momencie obserwowalne na dwuwymiarowej płaszczyźnie euklidesowej! Dla obserwatora z płaszczyzny euklidesowej parametry zmian (dane) dotyczące jej kolejnych skrętów) są „zmiennymi ukrytymi" w wyższej wymiarowości. Sprawdźmy dwa przejścia (przeskoki) fazowe:
W pierwszym przypadku, gdy zmienia się geometria z
2 π 1
na
4 π ½
mamy do czynienia z krzywizną dodatnią okręgu, a nie przestrzeni czy płaszczyzny odniesienia,
a w drugim, gdy geometria zmienia się z
2 π 1
na
π 2
mamy do czynienia z krzywizną ujemną okręgu, a nie przestrzeni czy płaszczyzny odniesienia.
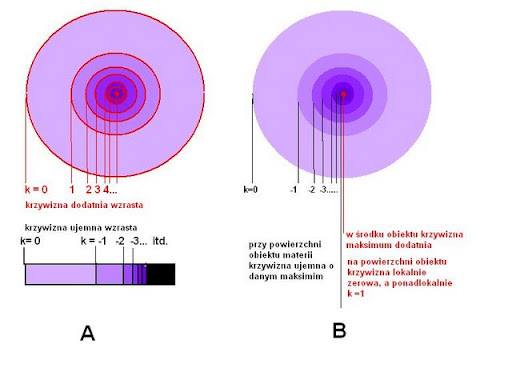
Oto jak nowa geometria uwzględniająca wymiar krzywizny wyjaśnia przyśpieszenia i możliwość zmiany częstotliwości spowodowanej wzrostem energii.
rys.
M.M.Boratyńska

